词法分析

词法分析 Lexical Analysis

• 计算机视角的代码

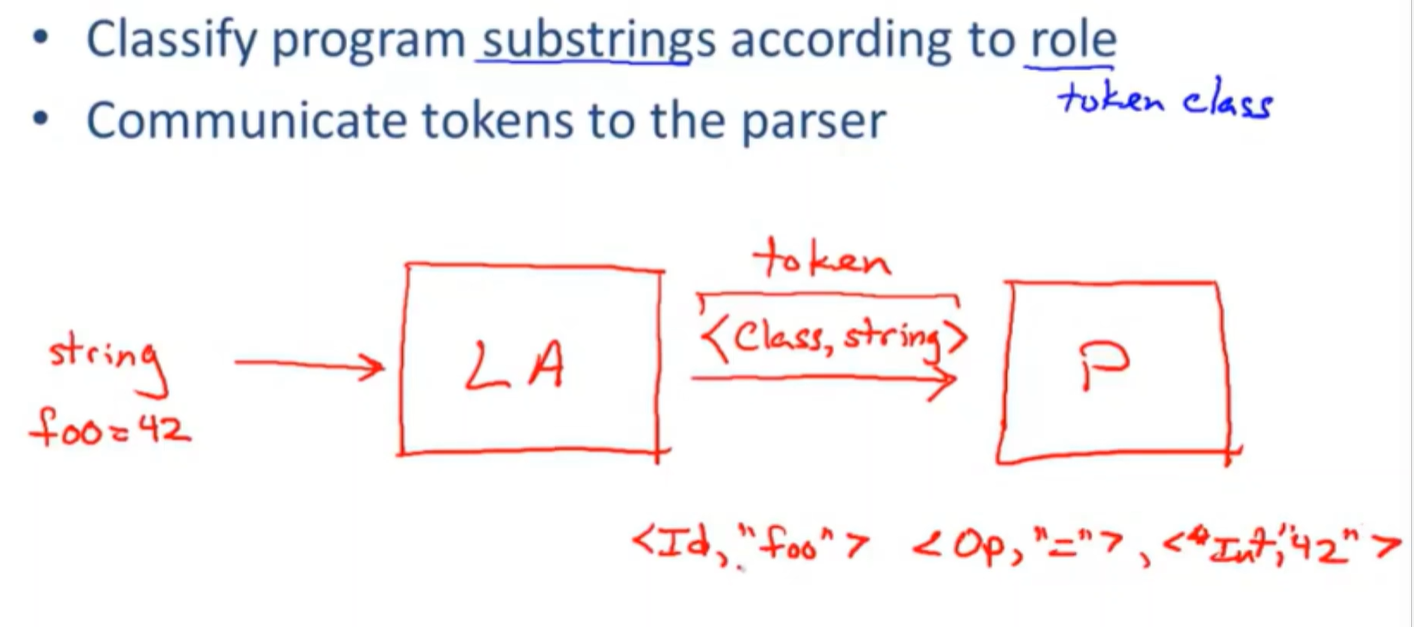
• class of the token:

token classes correspond to sets of strings

• identifier,keywords,’(’,’)‘,numbers
• identifier:strings of letters or digits,starting with a letter
• integer:a non-empty string of digits
• keyword:else if begin
• whitespace:a non-empty sequence if blanks,newlines,and tabs

• token<class,string>

• 标点符号自己一个就是一个类

• 3个组合成一个whitespace

• 需要做的事情：

• recognize substrings corresponding to tokens:substrings 被称为词素，构成词的要素。the lexemes

• identify the token class of each lexeme

• 输出为词法单元，a pair <tokenclass,lexeme>

LA Examples

• fortran rule:white space insignificant.加上去掉空格没有影响。^为什么会有这一给规则？punch card machine 应用于。很容易 不小心添加空格
• 标点的影响，label 5,variable i
• do是关键字还是变量名。需要从左往右lookahead,看到,才知道是什么
• 最小化lookahead数量，最好限制在某个常量。

PL/1 programming languages 1:ibm

• feature: keywords are not reserved

• keyword 与variable

• 因为declare后面的参数数量不确定 所以lookahead的数量也是不确定的

• 嵌套的模板 添加空格修复此法分析

Regular languages

• base

  • single character
  • epsilon

• compound

• union

• concatenation

• iteration:A*=A^i i>=0

Formal Languages

计算理论 a formal language is any set of strings over some aplhabet.

• alphabet=ascii,language=c program
• meaning function l maps syntax to semantics:l(e)=m[exp ,meaning]

例子

$ϵ$={” ”} ‘c’={“c”} A+B=AUB AB+{ab|a属于A并且b属于B} A*=U $A^i$ expr=set

• meaning function存在是为了使定义更清晰
• L：Exp→sets of strings

so why use a meaning function

• makes clear what is syntax,what is semantics
• allows us to consider notation as a seperate issue
• experessions and meanings are not 1-1,多对一

Example

罗马数字的例子，四则运算困难；阿拉伯数字 ；改变了notation,符号系统 是重要的,government how you think, what you can say.

0*，0+0*，$ϵ$+00*,$ϵ$+0+0*

• 是编译优化的基础，不同程序在功能上是等价的，allows us toreplace one program for another 运行更快且执行结果完全相同
• 如果是一对多，那就说明写了模棱两可的程序

lexical specifications

< 如何使用正则表达式来定义编程语言的各个不同方面

• keyword:“if” or “else” or “then” or …
  • ‘if’ +‘else’+‘then’+…,union then altogether
• integer: a non-empty string of digits
  • 首先，写数字：digit=‘0’+‘1’+‘2’+…
  • 多个数字 digit*,但是不能为空 digitdigit*,at least one digit=digit+
• identifier:strings of letters or digits,starting with a letter
  • letter=‘a’+‘b’+…=character range[a-zA-Z]union of all single chracter
  • letter(letter+digit)*,begin with a letter,followed by 0 or more letters and digits
• whitespace:a non-empty sequence of blanks,newlines,and tabs
• ’ ’+‘\n’+‘\t’ 通过naming 表达这些排版很差的字符
• 并集加括号加加号 （’ ’+‘\n’+‘\t’）+

其他领域 email

anyone@cs.stanford.edu 被标点符号分割

• letter+’@‘letter+’.’ letter+’.’ letter+1

pascal的例子

• 分数和指数
• 这个数字的分数部分可以存在或不存在 opt,对$ϵ$并集。两种写法
• 
• 指数 sign

总结

lexical specification again

redo - 词法规则由一堆用于token类的

Finite Automata

• 正则表达式=词法规范
• 有限自动状态机=实现
• accepting state=终止态
• a finite automaton consists of
  • an input alphabet $\sum$
  • a set of finite states S
  • a start state n
  • a set of accepting states $F\subseteq S$
  • A set of transition state -input→state

transition

• in state s1 on input a go to state s2
• get stuck:发现自己处于一种无论输入什么都不会发生转换的状态
• 两种情况，到达输入的末尾但是自动机未处于最终状态，或者由于卡住而永远不会到达输入的末尾

notation

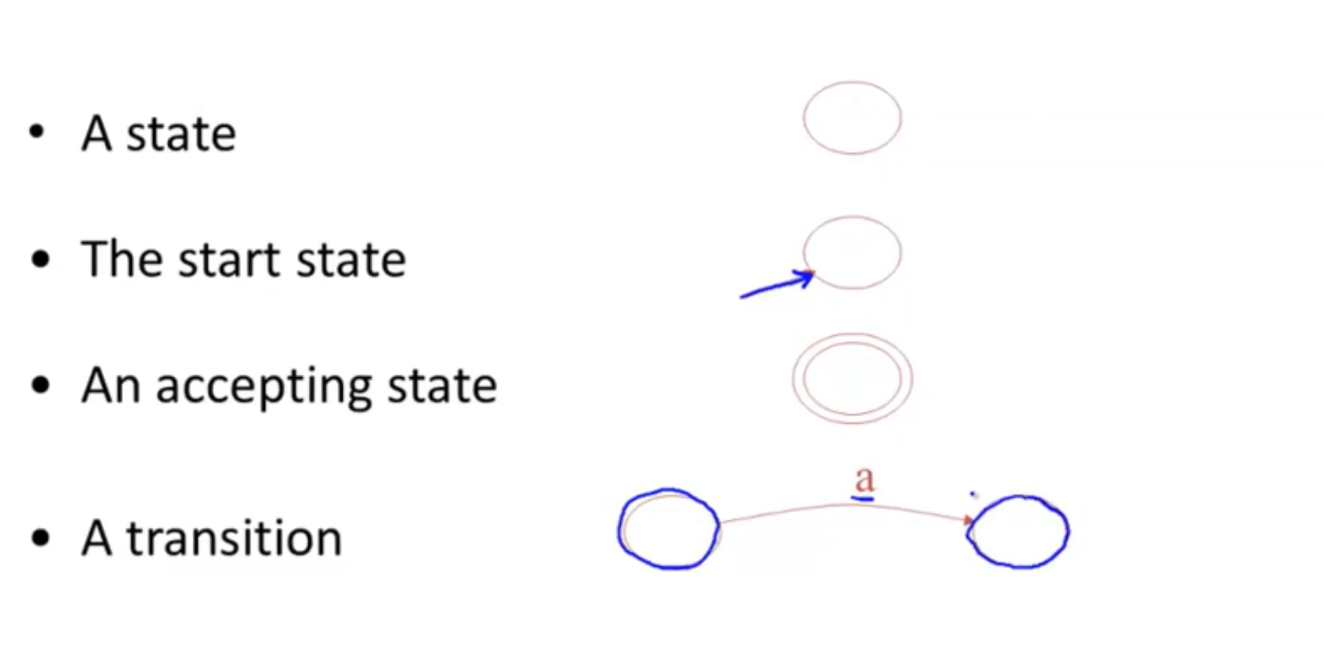
• 首先 一个开始状态 一个结束状态，问题是两者之间放什么，转换。
• 输入指针永远向前移动
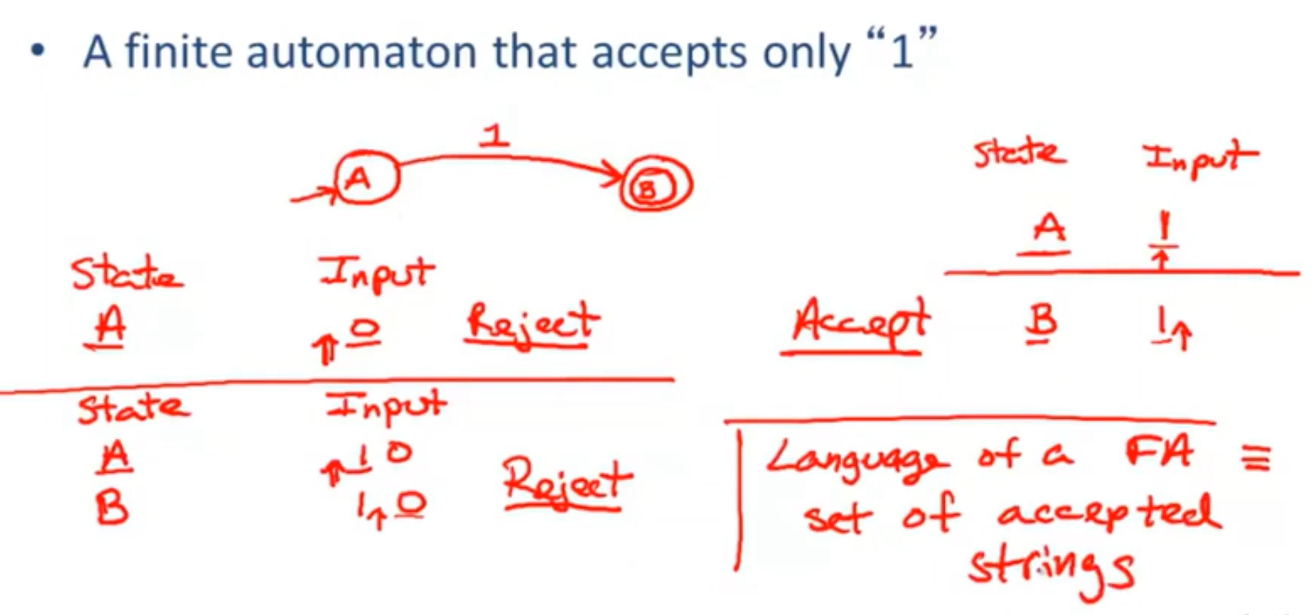
• 有限自动状态机语言 指的是自动机接受的字符串的集合

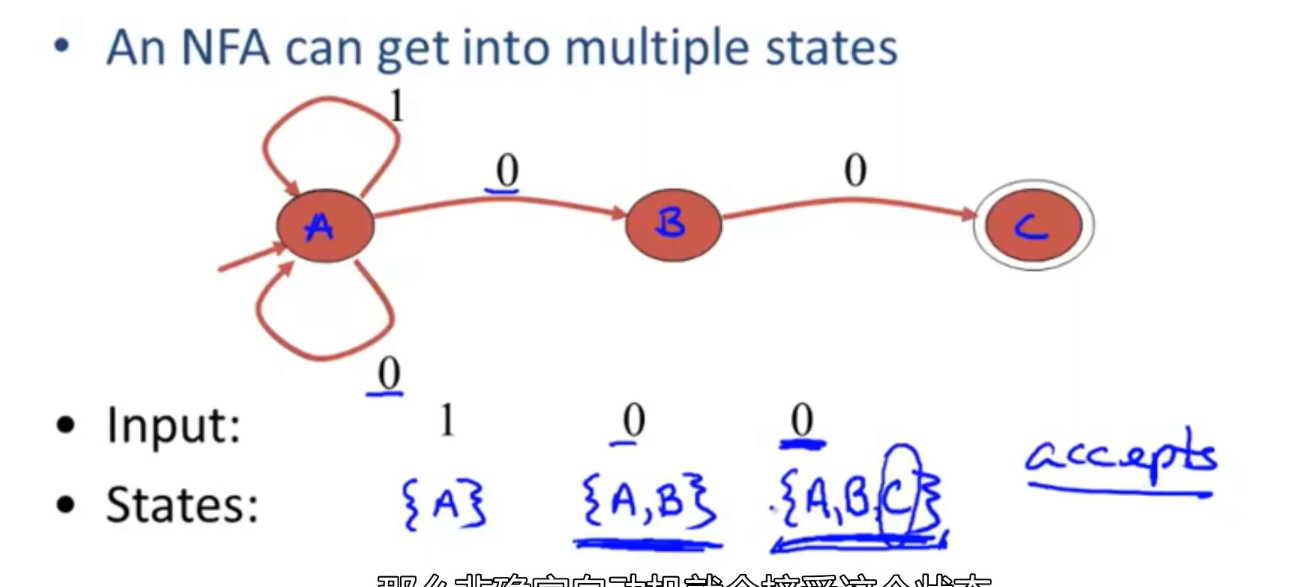
另一个例子

• 极端情况，没有1
• 初始的配置条件：一个包含了初始状态和地址的指针和一个Input指针

另一种transition:$ϵ$-moves

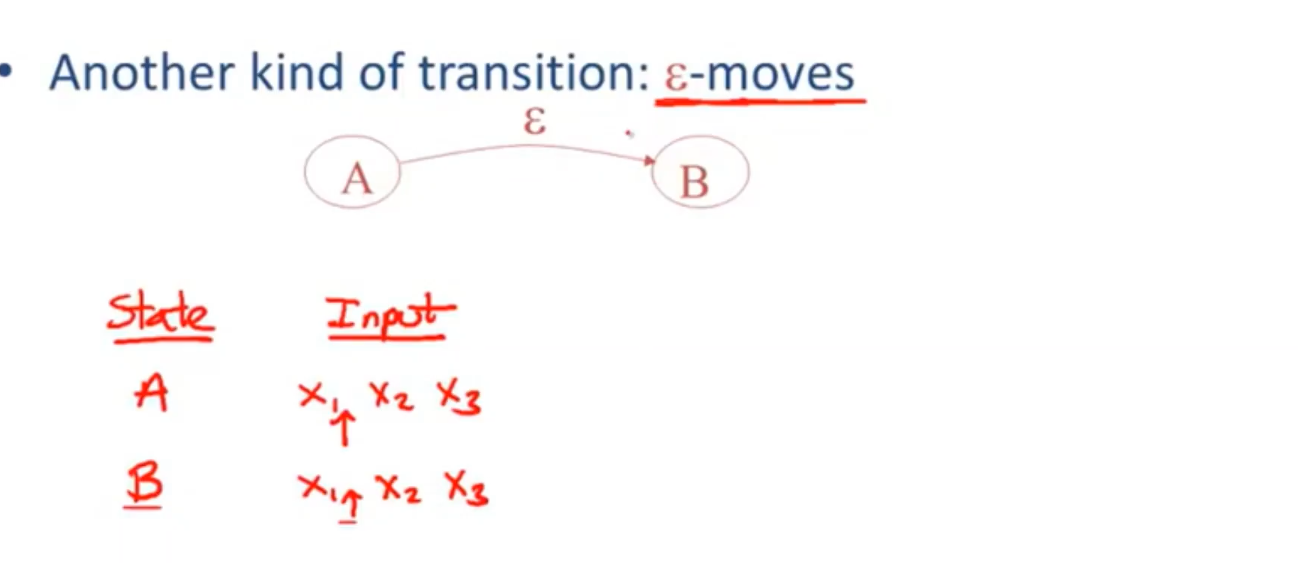input pointer 不动。空跳，无消耗移动，可以移动到其他状态而无需消耗任何输入

DFA

两个属性： 区别是空调，一个输入对应多种输出

• a dfa takes only one path through the state graph
• an nfa can choose; it acepts if some choices lead to an aceepting state

根据nfa不同选择 能够进入对应的不同状态

----------

总结

• NFAs and DFAs recognize the same set of languages(regular)
• DFAs are faster to execute(there are no choices to consider)
• NFAs are in general smaller(exponentially)
• 两者是时空上的tradeoff,一个执行速度快，一个小

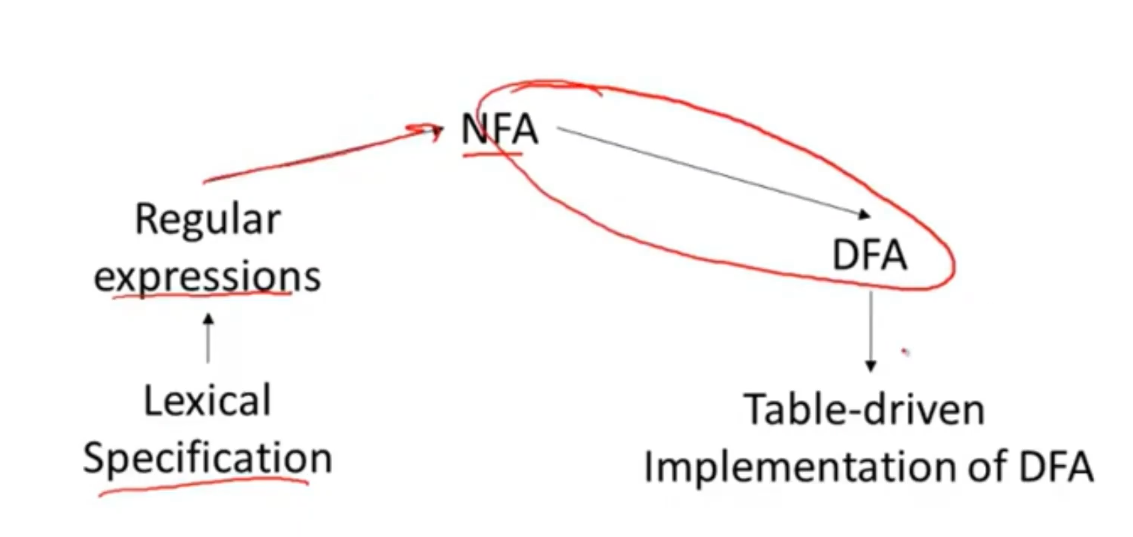
Regular Expressions to NFAs

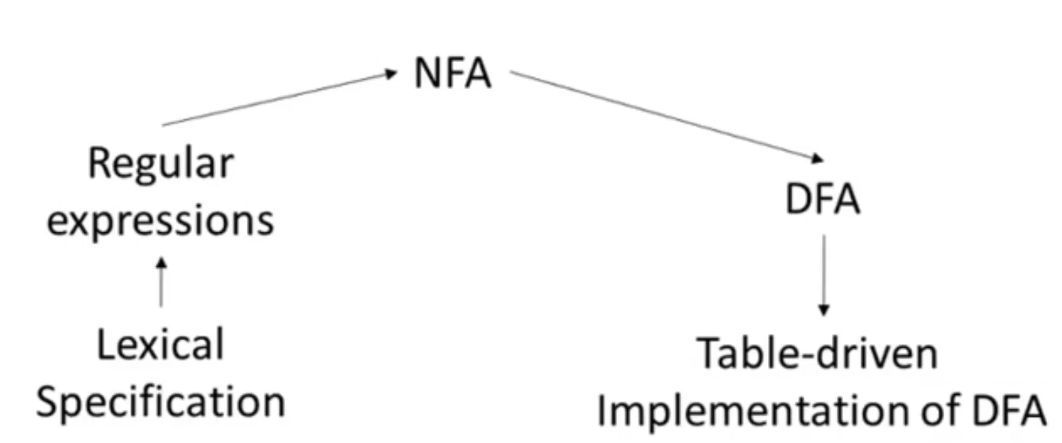主要流程 构建一个词法分析器的流程图

• 这一节是从 正则表达式 转换为 NFA
• for each kind of rexp,define an NFA
  • notation: NFA for rexp M
• 红色箭头 一：开始；二：结束
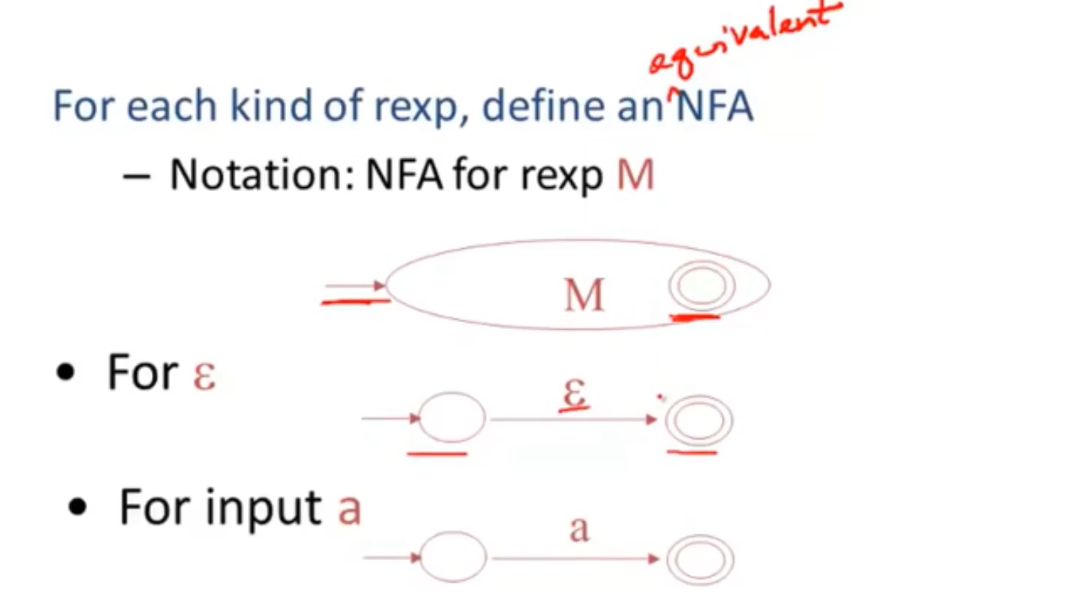
• 复合表达式
  • AB
  • A+B union of a and b compound machine这个输入是术语自动机A所接受的语言 或者是自动机B所接受的语言。从 开始状态立即决定是属于A语言还是B语言
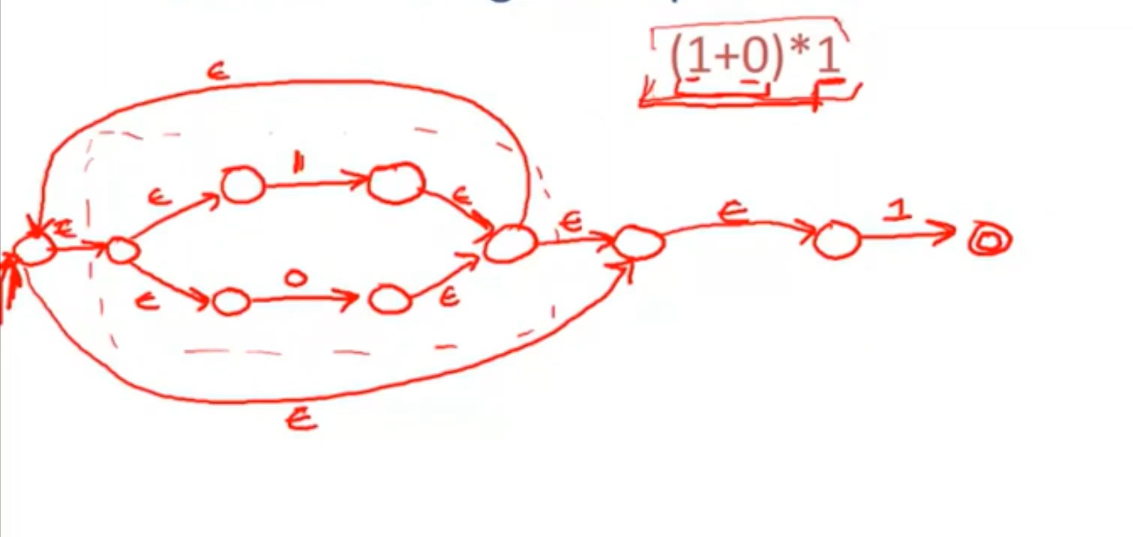
• 迭代 最复杂的情况 A* 识别0个或多个A
  • 空字符串 从起始状态到最终状态
  • 在自动机A的最终状态通过空跳回到整个自动机的开始状态，或者转换到机器的最终状态
• 归纳的方法 从简单到复杂
  • 例子：（1+0）*1
  • 一个自动机接受0/1 ，然后整合进一个自动机 既接受1又接受0，通过空跳回到这个组合自动机的最终状态。然后进行迭代。
  • 构建另一个自动机接受1.

从 NFA 到 DFA

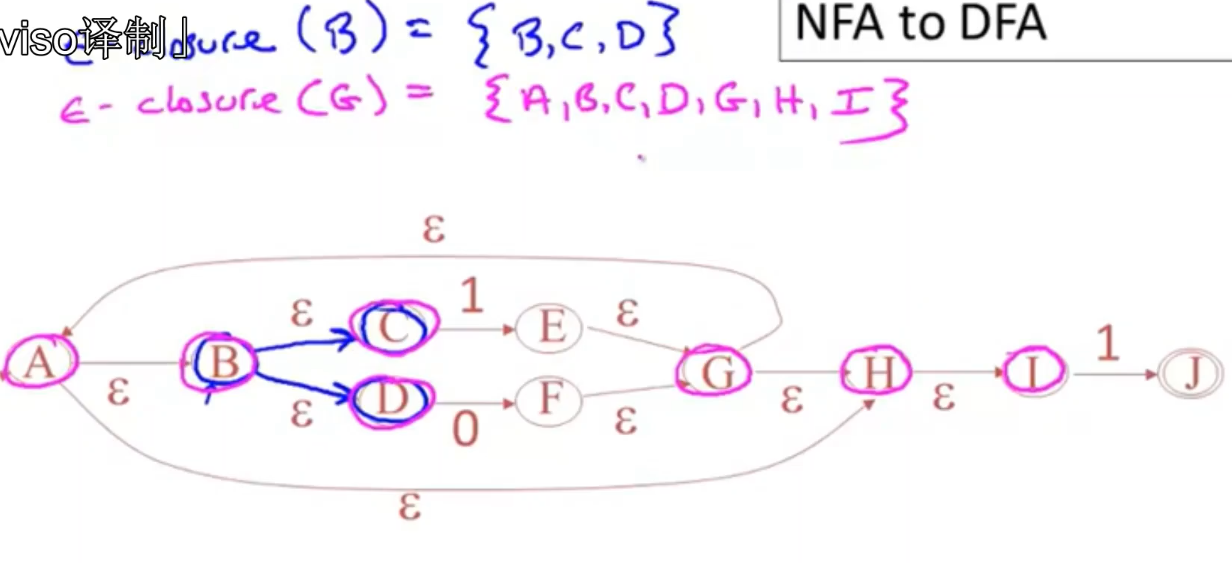
$ϵ$ closure

• 只通过空跳就可以到达的状态。

how many different states an nfa may be in

• N个状态。非空子集为$2^N-1$ .
  • 首先，这个数很大，nfa会得到大量不同状态的组合。
  • 其次，it is a finite set of possible configurations因此为nfa转换为dfa提供了idea.尽管非确定自动机状态组合集合数量很大，它也只能获取到这个集合中的组合，这也是在构建确定自动机所要利用的特性

方案：将任意一个非确定性有限自动状态机映射到一个等效的确定性有限自动机

NFA

• states S
• start s属于 S
• final F 是S的子集
• 转换函数transition function：给定一个状态集X，展示通过输入字符a可以到达的所有状态。a(a character) apply to a set of states. 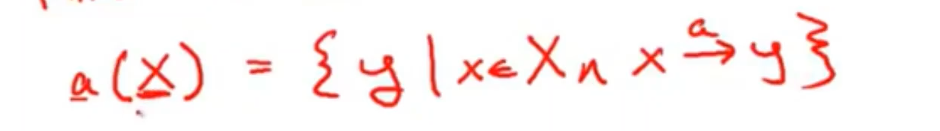todo
• $ϵ$ -closure

DFA

• states subsets of S(除去空集) 虽然大，但是是有限的>DFA的状态记录了NFA基于相同输入可能进入的可能状态集
• start state： $ϵ$ -clos(s)
• final {X|XintersectF不等于 空集}
• transition function: X-a→Y if Y=$ϵ$-close(a(X)) > 基于每个输入，每个状态都只会有一个可能的移动路线

例子

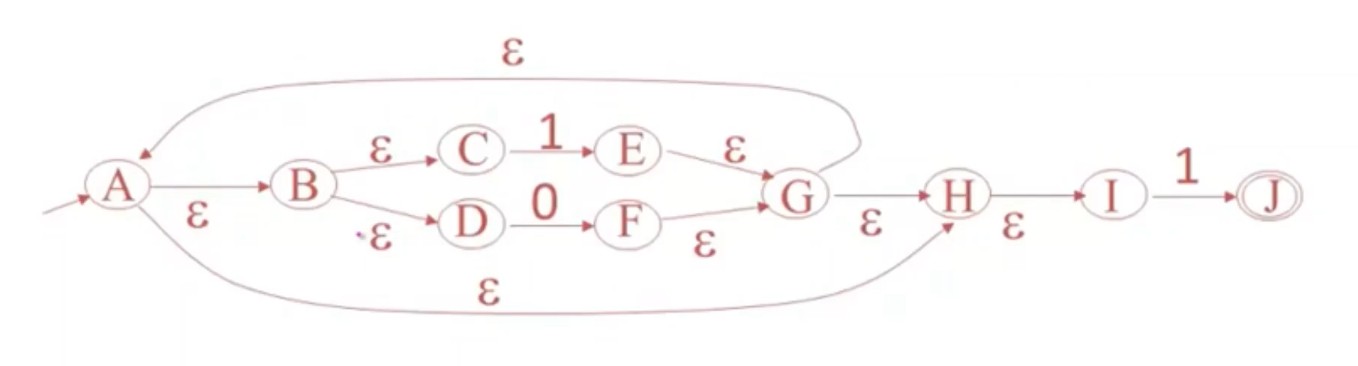
• 从开始状态A开始，紫色

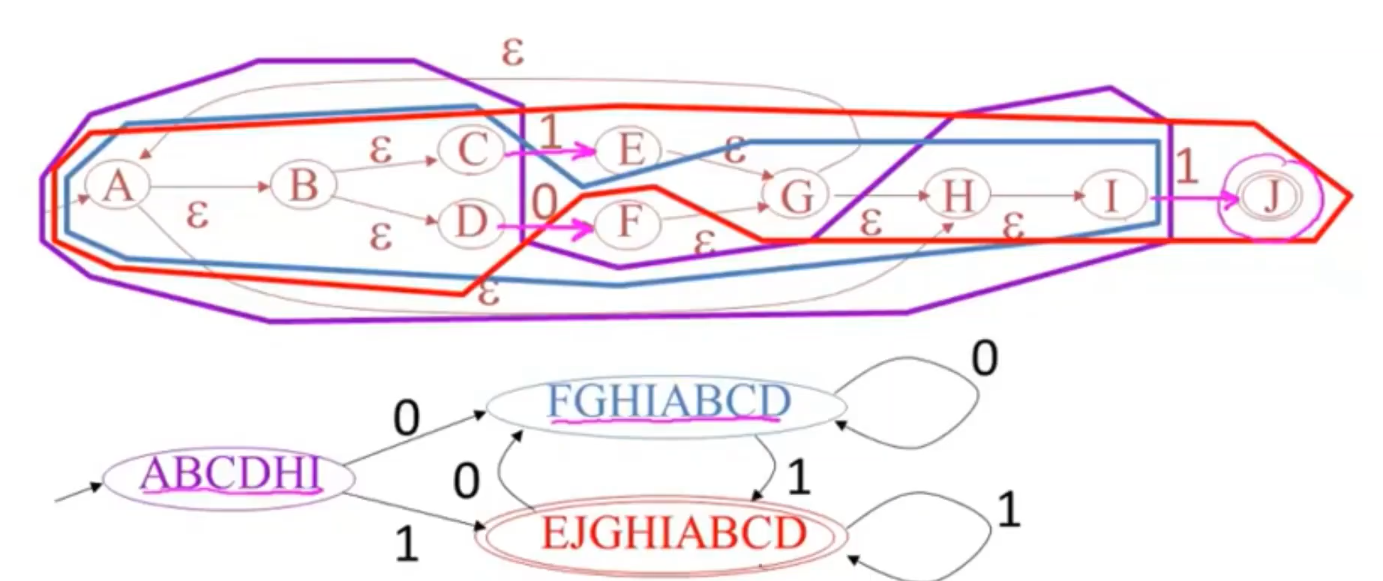
实现有限状态机 implementing finite automata

• a DFA can be implemented by a 2D table T 二维数组的形式
  • 一个维度是状态
  • 另一个维度是输入符号
  • for every transition Si⇒a Sk defineT[i,a]=k

例子

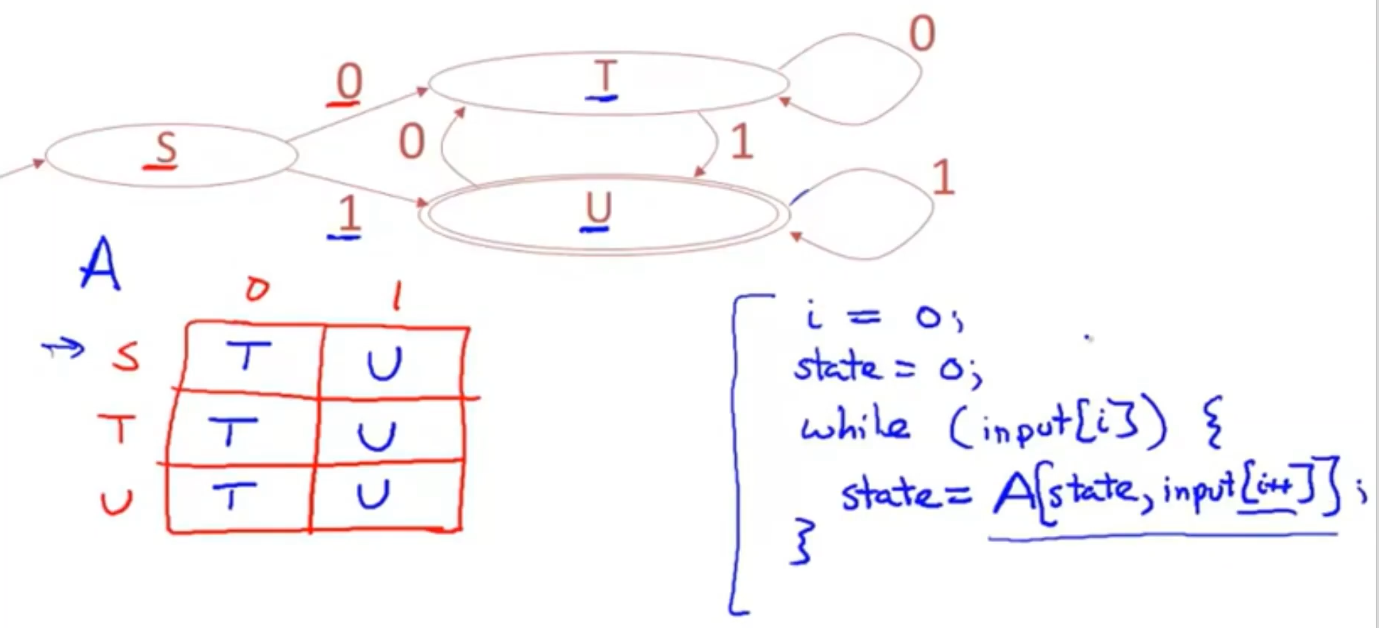i=0;(input index)state=0(当前状态);while ，我们想要做的是对输入进行遍历，并对其检查，对输入的每个元素是否需要进行一次转换，在输入为空时停止。 while(input[i]) 当数组中的元素不为空时 ，在每一步更新状态，怎么更新？在转换关系数组A中进行查找，如何查找？先查找当前状态，再去查找输入，通过使用当前状态和当前输入，我们就能确定一个新的转换状态。同时，输入指针自增。loop that processes an input according to the transiton table A

• 这是一个compact ,efficient process。只需 一点 索引计算，和两张表lookups,one for the input,one for the state transition table per character input
• 缺点：有大量重复行
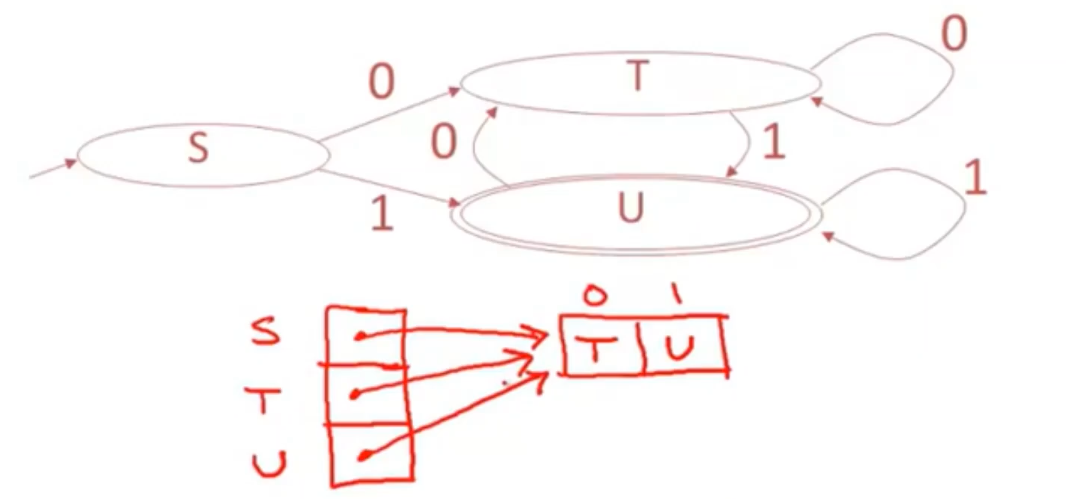
• 改进：使用一维表，指针指向移动的状态。共享行。
• 事实证明，在用于词法分析的自动机中，重复行非常常见，状态很多的,2^n -1
• 直接使用NFA

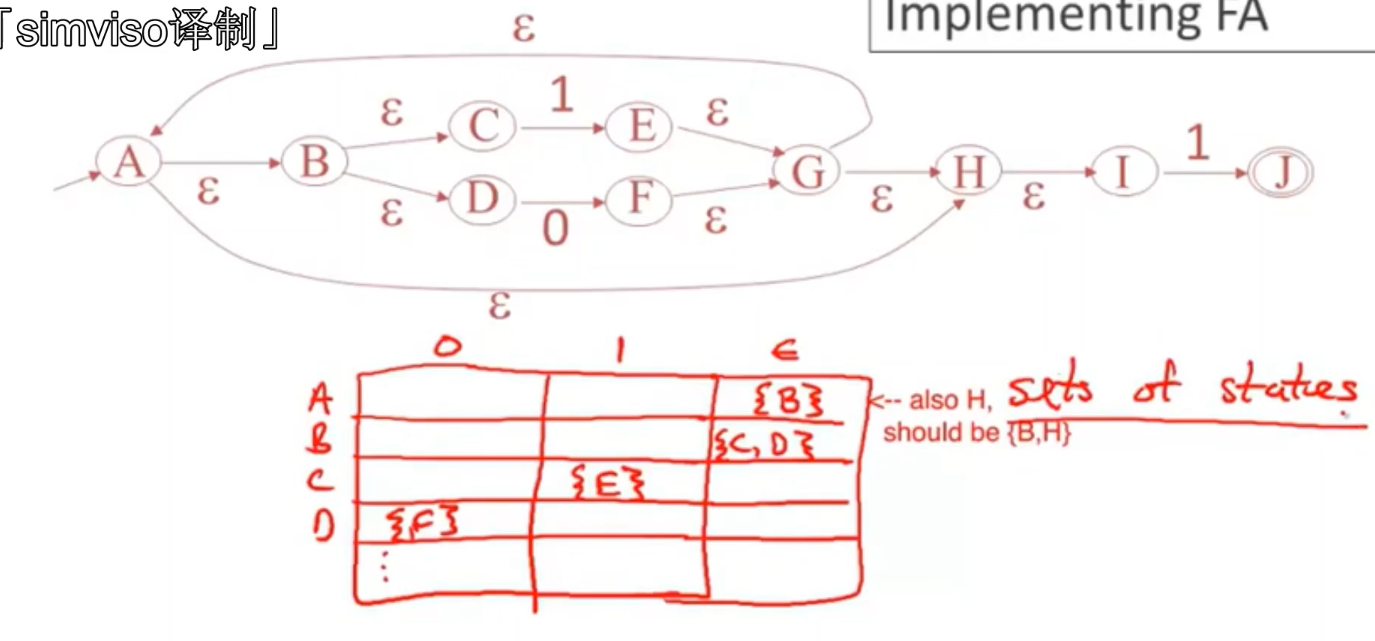
summeraize

• 实现词法规则的关键思想时 将非确定性有限自动机转换为确定性有限自动机
• tools trade between speed and space
  • dfa faster（执行速度） less compact(表可能会很大)
  • nfa slower more concise