语法分析

Abstract Syntax Trees

core data structure used in compilers

a parser traces the derivation of a sequence of tokens;跟踪一系列词法单元的推导
But the rest of the compiler needs a structural representation of the program
Abstract Syntax Trees
- like parse tree but ignore some details
- abbreviated as AST
太多冗余的信息。括号，只有一个孩子节点的节点。
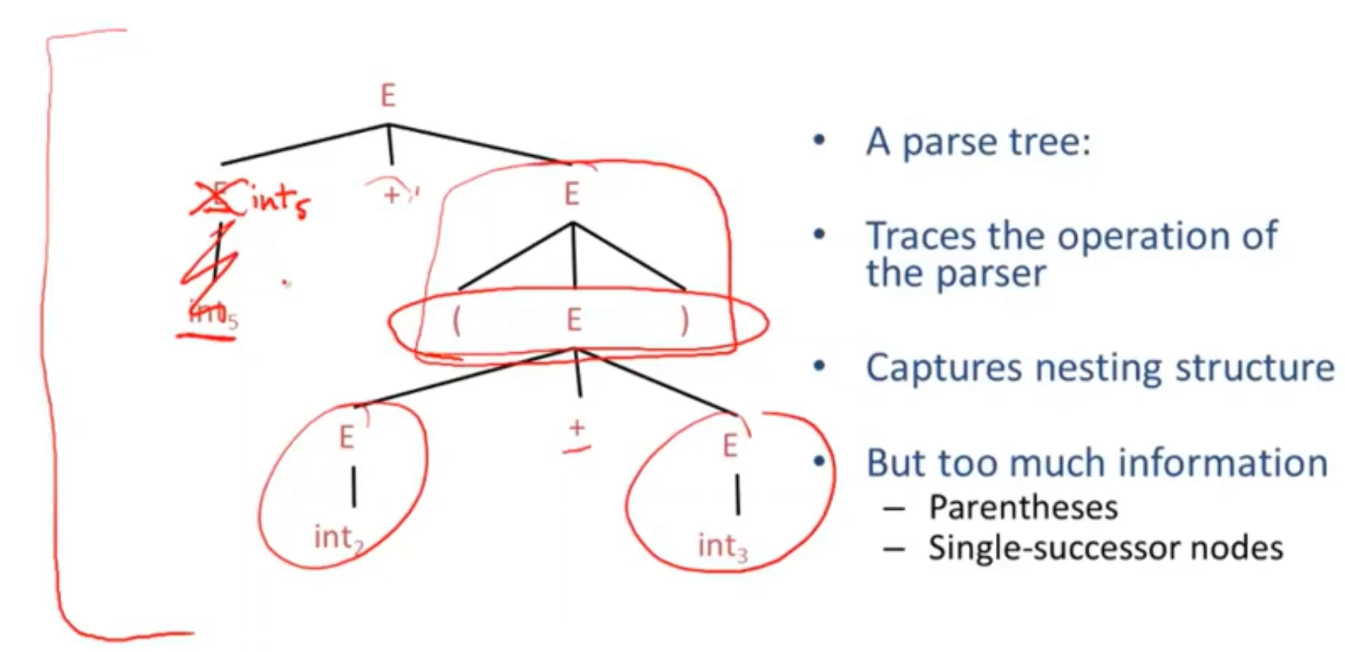
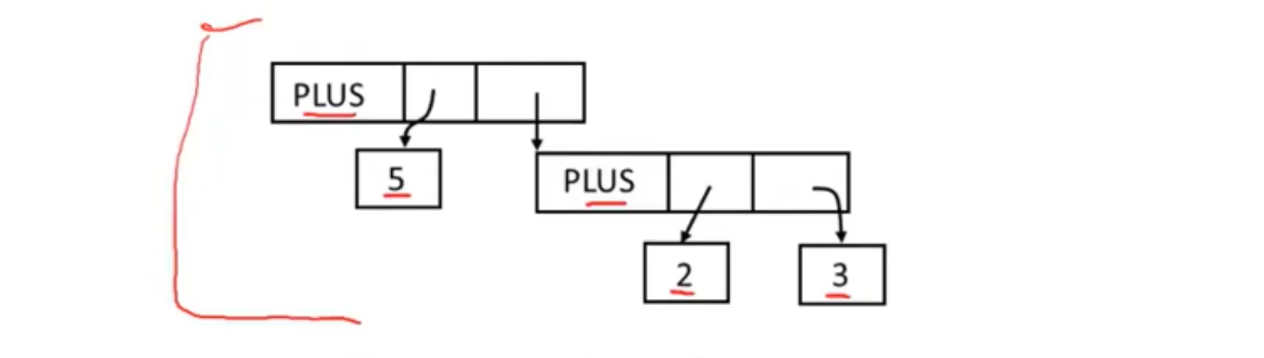
同样也捕获了了嵌套的结构
但是抽象了具体的语法
- more compact and easier to use
an important data structure in a compiler

recursive descent parsing递归下降

第一个parsing algorithm

the parse tree is constructed from the top down from left to right 一个一个产生式尝试。只要不是生成的终结符号就不知道自己对不对。三部分：产生式；解析树；输入，指针；。不对的话 backtrack,回退。

RD Algorithm

define some small things used

let TOKEN be the type of tokens
- special tokens INT,OPEN,CLOSE,PLUS,TIMES（类型值）
let the global next point to the next input token

here we go

Define boolean functions that check for a match of:
- a given token terminalbool term(TOKEN tok){return *next++==tok;}//side effect 指针向前移，不管是否匹配
- the nth production of S:bool Sn(){...}
- try all productions ofS:bool S(){...}任意一个匹配。

例子

For production E→Tbool E1(){return T();}
For production E→T+Ebool E2(){return T()&&term(PLUS)&&E();}注意每次调用函数后指针的移动；第二个产生式子
For all productions of E(with backtracking)我们唯一担心的状态是next指针。如果我们撤销我们的决定，那么它需要被恢复```

bool E()
{
	TOKEN *save=next;
	return (next=save,E1())||(next=save,E2();)
}//第一个next=save其实可以去掉，但为了整齐

Functions for non-terminal T
每一步，还原输入指针

limitation of rda

语法+实现（一组相互递归的函数共同实现这个简单的递归下降策略）

当我们去解析输入Int时会发生什么
输入int *int rejected,what happened?在我们尝试为一个非终结符元素找到一个合适的产生式时，可以使用backtracking,回滚处理，但是一旦我们找到一个能够用在非终结符元素的产生式的话，就没有了回滚操作，不能尝试a diffrent production.

the problem

if a production for non-terminal X succeds
- cannot backtrack to try a different production for X later
general recursive-descent algorithms support such full backtracking
- can implement any grammer
presented recursive descent algorithm is not general
- but is easy to implememt by hand
sufficient for grammers where for any non-terminal at most one production can succeed
the example grammar can be rewritten to work with the presented algorithm
- by left factoring,the topic of a future video

Left Recursion

the main difficulty with rd

consider a production S→S a bool S1(){return S() && term(a);} bool S(){return S1();}

问题

当我们去解析一个输入字符串的时候，调用 S()→S1()→S1()…,结果是陷入一个无限循环。原因： a left-recursive grammer has a non-terminal S S→+ Sa,+表示多次重写。

$S \to S α ∣ β$ 该语法。

S genrates all strings starting with a beta and followed by any number of alphas.最后生成第一个字符。没办法用于递归下降Parsing 从左到右 但是这个语法却是按照从右到左的顺序构建字符串的

Idea

can rewrite using right-recursion
$S \to β S^{'} S^{'} \to α S^{'} ∣ ϵ$

S prime 产生一连串的alpha,也可以是空序列

左递归变为右递归基本形式

In general $S \to S α_{1} ∣...∣ S α_{n} ∣ β_{1} ∣...∣ β_{m}$
all strings derived from S start with one of B1,…,Bm and continue with several instances of a1,…an
rewrite as

S \to β_{1} S^{'} ∣...∣ β_{m} S^{'} S^{'} \to α_{1} S^{'} ∣...∣ α_{n} S^{'} ∣ ϵ

immediate 中间左递归

the grammer

S \to A α ∣ δ A \to Sβ

is also left-recursive because $S \to + Sβ α$ 花两步就生成了另一个在左侧有S的字符串

summary

recursive desenct
- simple and general parsing strategy
- left-recursion must be eliminated first
- …but that can be done automatically
used in production compilers
- gcc frontend 手写的递归下降解析器

predictive parsing

like recursive-descent top down parser,but parser can predict which production to use
- by looking at the next few tokens use lookahead,restricted grammers
- no backtracking involvedadvantage,完全肯定要使用的产生式，completely deterministic,never try altenatives
predictive parsers accept LL(k) grammars
- left to right
- left-most derivation
- k tokens lookahead
in recursive descent
- at each step,many choices of production to use
- backtracking used to undo bad choices
in LL(1)
- at each step,only one choice of production
recall the grammar
$E \to T + E ∣ T T \to in t ∣ in t * T ∣ (E)$
hard to predict because
- for T two productions start with int
- for E it is not clear how to predict
we need to left-factor the grammar 提取左公因子

idea

消除一个非终结符的多个产生式的公共前缀使用一个产生式来处理这个前缀为这些不同后缀引入一个非终结符

parsing table -right hand side

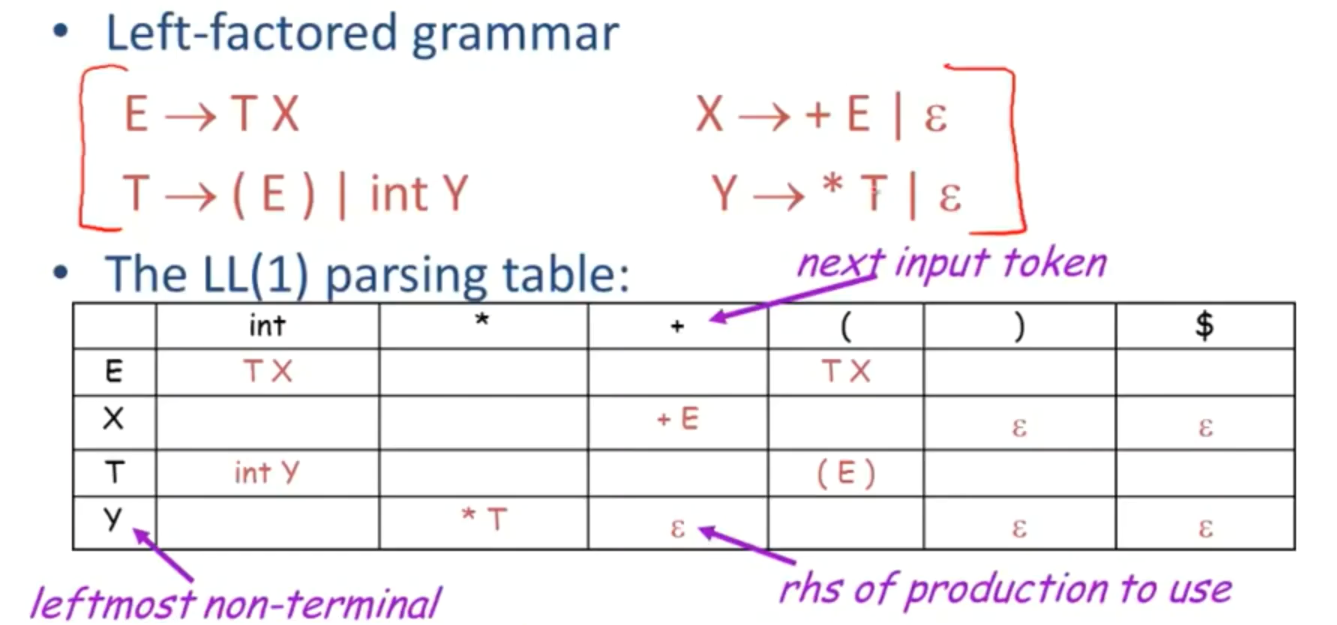
找到当前非终结符为E，同时下一个输入是int,entry[E,int]：若当前非终结符是E并且下一个输入是int 那么使用产生式E→TX;
[Y,+]输入为+，且当前最左非终结符为Y时，成功解析的唯一途径是Y不生成任何东西。若当前非终结符是Y并且token是+那么甩掉Y。get rid of Y
空的单元格，即错误单元格。[E,*] :there is no way to derive a string starting with * from non-terminal E.

使用解析表进行解析的算法

方法与递归下降类似，除了
- 除了需要看最左边的非终结符S，我们还要看下一个输入token:a.choose the production shown at [S,a]
不使用递归函数去trace out parse tree,a stack records frontier of parse tree.树的叶子节点。边界
- non-terminals that have yet to be expanded
- terminals that have yet to matched against the input
- top of stack该栈最重要的属性 最左终结符或非终结符始终放在栈顶。leftmost pending terminal(trying to match) or non-terminal(trying to expand)
reject on reaching error state .遇见一个错误状态，拒绝解析
accept on end of input&empty stack

initialize stack=<S$> and next
repeat
case stack of
<X,rest>: if T[X,*next]=Y1...Yn
			then stack<-- <Y1...Yn rest>;
			else error();//空格
<t,rest>: if t==*next ++
			then stack<--<rest>;
			else error()
until stack== < >

First Sets

how to construct parsing table(或者说，构建ll(1)解析表所需要的条件)

consider non-terminal A(left most),production A→a,&token t
T[A,t]=a in two cases:
第一个情况 $α \to * tβ$ ：a可以推导出t在第一个ie位置。a can derive a t in the first position,we say that $t \in F i rs t (α)$
另一种情况， $α$ 不能推导出t,说明t不是a的first 集。但是如果a可以为 $ϵ$

definition

$F i rs t (X) = {t ∣ X \to * t a} \cup {ϵ ∣ X \to * ϵ}$ 我们需要记录 x是否会生成 $ϵ$

algorithm sketch:

First (t)={t} t is a terminal
$ϵ \in F i rs t (X)$
1. if X→ $ϵ$
2. if $X \to A_{1} ... A_{n}$ and $ϵ \in F i rs t (A_{i})$ for $1 \leq i \leq n$ .x在产生式右手边生成其他元素，并且这些都能变成 $ϵ$ 的话，整个产生式右手边都能变成 $ϵ$
$F i rs t (α) \subseteq F i rs t (X)$ if $X \to A_{1} ... A_{n} α$
1. and $ϵ \in F i rs t (A_{i}) f or 1 \leq i \leq n$ 终结符以及非终结符的first集合

例子

Follow Sets

definition

follw集并不取决于该符号产生什么，取决于该符号可以出现的位置，该符号在语法中的使用位置 $F o ll o w (X) = {t ∣ S \to^{*} βXt δ}$

intuition 直观方法

if X→A B then $F i rs t (B) \subseteq F o ll o w (A)$ b的first集就是a的follow集。当你有两个相邻符号时第二个符号的first集合中的元素是第一个符号的follow集合中的元素and $F o ll o w (X) \subseteq F o ll o w (B)$ 产生式末尾符号的follow集会包含产生式左手边符号的follow集
- if $B \to^{*} ϵ t h e n F o ll o w (X) \subseteq F o ll o w (A)$ 如果 B能够消失
- if S is the start symbol then \in$ Follow(S).初始条件，特殊case

algorithm sketch

follow集不考虑 $ϵ$ ，是终结符的集合

example

终结符与非终结符的follow集合。两个互为子集，相等。

LL(1) parsing tables

目标

goal:construct a parsing table T for CFG G

流程

this is done by production.for each production A→ $α$ in G do
- 消除A

例子

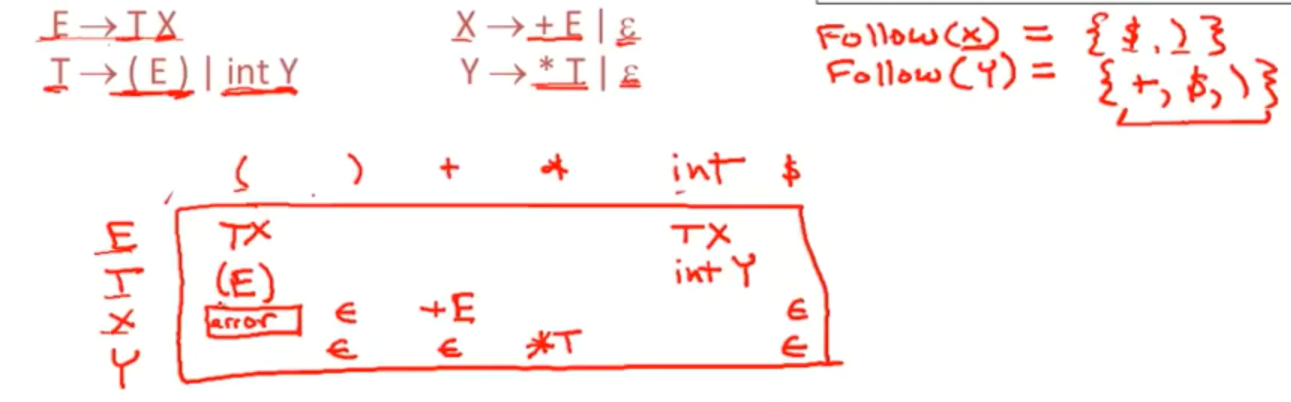
LL(1)parsing tables

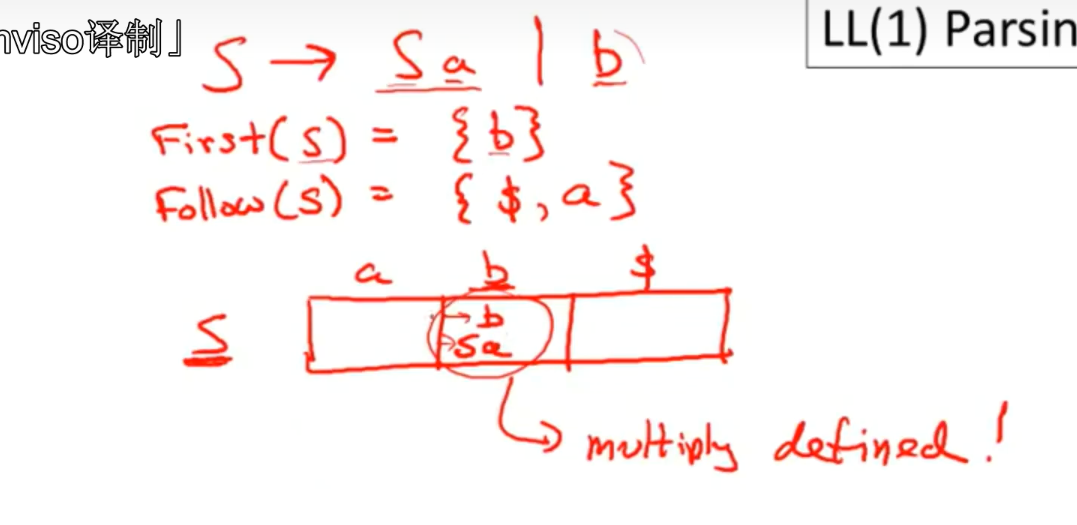
如果一个格子里有多个选择动作那么这个语法就不是LL(1)。
1. not left factored,不能提取左公因式
2. left recursive
3. ambiguous 语义
most programming language CFGs are not LL(1) .太弱的语法。

bottom-up parsing

bottom-up parsing reduces a string to the start symbol by reverting productions
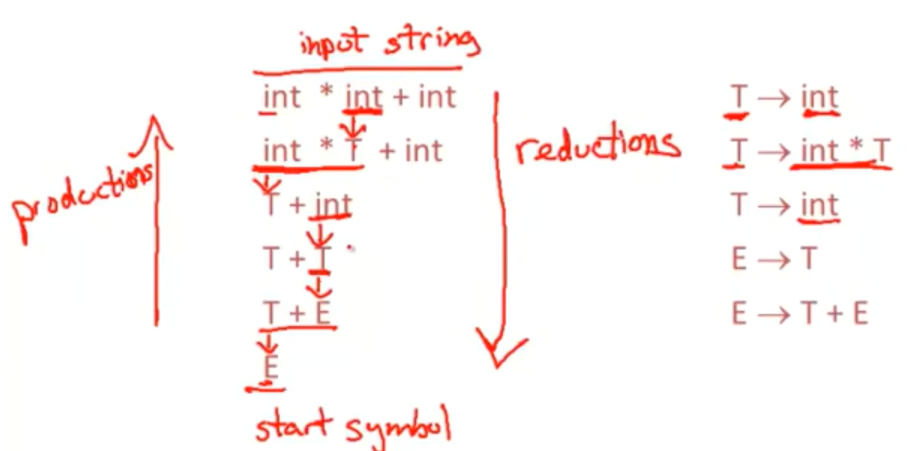
自下而上解析的另一种有趣属性：note the productions read backwards,trace a rightmost derivation
important Fact #1 about bottom-up parsing：
- a bottom-up parser traces a rightmost derivation in reverse

shift-reduce parsing

自下而上解析使用两种动作，shift and reduce

shift

read one token from input,表明解析器知道了下一个终结符是什么，解析器可以对它进行匹配以实现归约的目的

reduce

对竖线右侧字符串的右端末尾逆向使用产生式

实现

冲突

shift reduce;reduce reduce;

Handles

review

bottom-up parsing uses two actions:

shift:ABC|xyz⇒ABCx|yz,读取完一个token后，并将竖线向右移动一个token
reduce:Cbxy|ijk⇒CbA|ijk ,用产生式右边的内容替换产生式左边的内容
left string can be implemented by a stack,竖线左边字符串能够用一个栈来实现，栈顶的元素用竖线进行标记
- top of the stack is the |
shift pushed a terminal on the stack
reduce
- pops 0 or more symbols off the stack
  - production rhs
- pushes a non-terminal on the stack
  - production lhs

key question:how do we decide when to shift or reduce?

Example

E→T+E|T T→int *T|int|(E)

考虑步骤int |*int+int
T→int,mistake,T*没有办法处理
即使栈顶元素是产生式右手边的内容，它也可能是一个错误的归约操作。

idea: want to reduce only if the result can still be reduced to the start symbol

解析器从右到左进行解析
如果这是一个最右推导
那么 $α β$ 是 $α β ω$ 的一个句柄，意思是在这种情况下将 $β$ 归约为X是ok的

handle的提出,what it is

Handles formalize the intuition（where it is okay to do reduction）
- a handle is a reduction that also allows further reductions back to the start symbol。一个归约点。
we only want to reduce at handles

important fact #2 about bottom-up parsing: in shift-reduce parsing,handles appear only at the top of the stack,never inside.所有操作都会在竖线左侧进行

informal proof 句柄只会出现在栈顶

informal induction on # of reduce moves

true initially,stack is empty
immediately after reducing a handle
- right-most non-terminal on top of the stack
- next handle must be to right of right-most non-terminal ,because this is a right-most derivation.无法再对最右非终结符的左边进行任何的归约操作
- sequence of shift moves reaches next handle
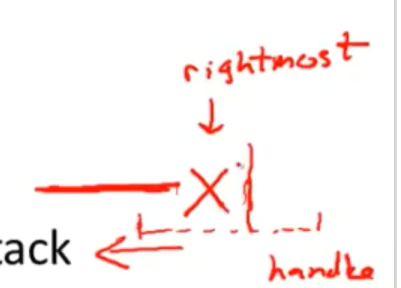
in shift-reduce parsing,handles always appear at the top of the stack
handles are never to the left to the rightmost non-terminal
- 因此，移位归约操作已经足够，the | need never move left
bottom-up parsing algorithms are based on recognizing handles

句柄识别

news

Bad news
- there are no known efficient algorithms to recognize handles
Good news
- there are good heuristics for guessing handles
- on some CFGs,the heuristics always guess correctly

文氏图

严格包含关系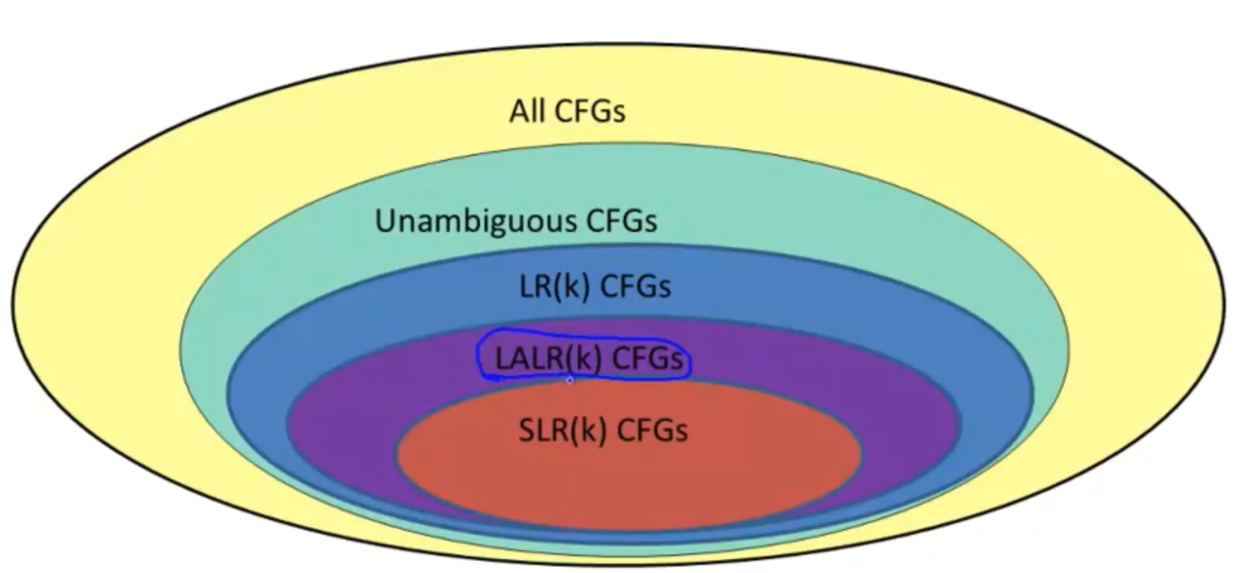

it is not obvious how to detect handles
so what does the parser know?
at each step the parser sees only the stack,not the entire input

Definition

$α$ is a viable prefix(可行前缀) if there is an $ω$ such that $α ∣ ω$ is a state of a shift-reduce parser。一个有效配置

what does viable prefix mean?

a viable prefix does not extend past the right end of the handle.不会延伸到句柄右端
it’s a viable prefix because it is a prefix of the handle
as long as a parser has viable prefixes on the stack no parsing error has been detected
比如 $α ∣ ω$ 是可行的 viable,说明我们没有遇到错误，这是shift-reduce解析中的一些状态。

important fact#3 about bottom-up parsing: for any grammar,the set of viable prefixes is a regular language对于任何语法来说，可行前缀集就是一个正则语言 keyto the bottom-up parsing,所有自下而上的解析器都是基于这个事实开发的。可行前缀集可以被有限自动机所识别。

how to compute automata that accept viable prefixes

Definition

an item is a production with a ”.” somewhere on the rhs

special cases: the only item for X→ $ϵ$ is X→.no symbol on the rhs

items are often called “LR(0) items”

the problem in recognizing viable prefixes is that the stack has only bits and pieces of the rhs of productions
- if it had a complete rhs,we could reduce
大部分时候，栈顶不会有一个完整的产生式右手边内容，只是部分。
在栈内的内容并不是随机的，它有一种特殊的结构。these bits and pieces are always prefixes of rhs of productions

example

consider the input(int)

E->T+E|T
T->int*T|int|(E)

then (E|)is a state of a shif-reduce parse,|前面是栈，后面是Input.有效状态
(E is a prefix of the rhs of T→(E)
- will be reduced after the next shift
item T→(E.)says that so far we have seen (E of this production and hope to see ).用来描述状况。记录了目前我们当前处理产生式的进度
.左侧内容是我们已经见过的，即栈内元素，.右侧是我们能够进行归约操作前我们想要读取的内容

the structure of the stack

the stack may have many prefixes of rhs’s

存储了产生式右手边前缀的栈，bunch of prefixes,stack up on the stack

let prefixi be a prefix of rhs of Xi→ai
- prefixi will eventually reduce to xi
- the missing part of ai-1 starts with xi
- i.e. there is a xi-1 → prefixi-1xiB for some B todo
recursively prefixk+1…prefixn eventually reduces to the missing part of ak

example

从底部开始。注意我们是如何通过对栈中元素进行处理使之最终变成产生式右侧一部分。T。

sum

idea: to recognize viable prefixes,we must

recognize a sequence of partial rhs’s of productions,where
each partial rhs can eventually reduce to part of the missing suffix of its predecessor

识别可行前缀 recognizing viable prefixes

自下而上型解析的技术亮点。算法。

算法

add a dummy production S’→S to G. 让事情变得更简单新开始符号只位于左边，仅在一个地方使用
the nfa states are the items of G
1. including the extra production
for item $E \to α . Xβ$ add transition.到目前为止，我们看到了a在栈上。
x为非终结符 for item $E \to α . Xβ$ and production $X \to γ$ add
every state is an accepting state
start state is s’→.s. 自动机的状态就是语法的Item

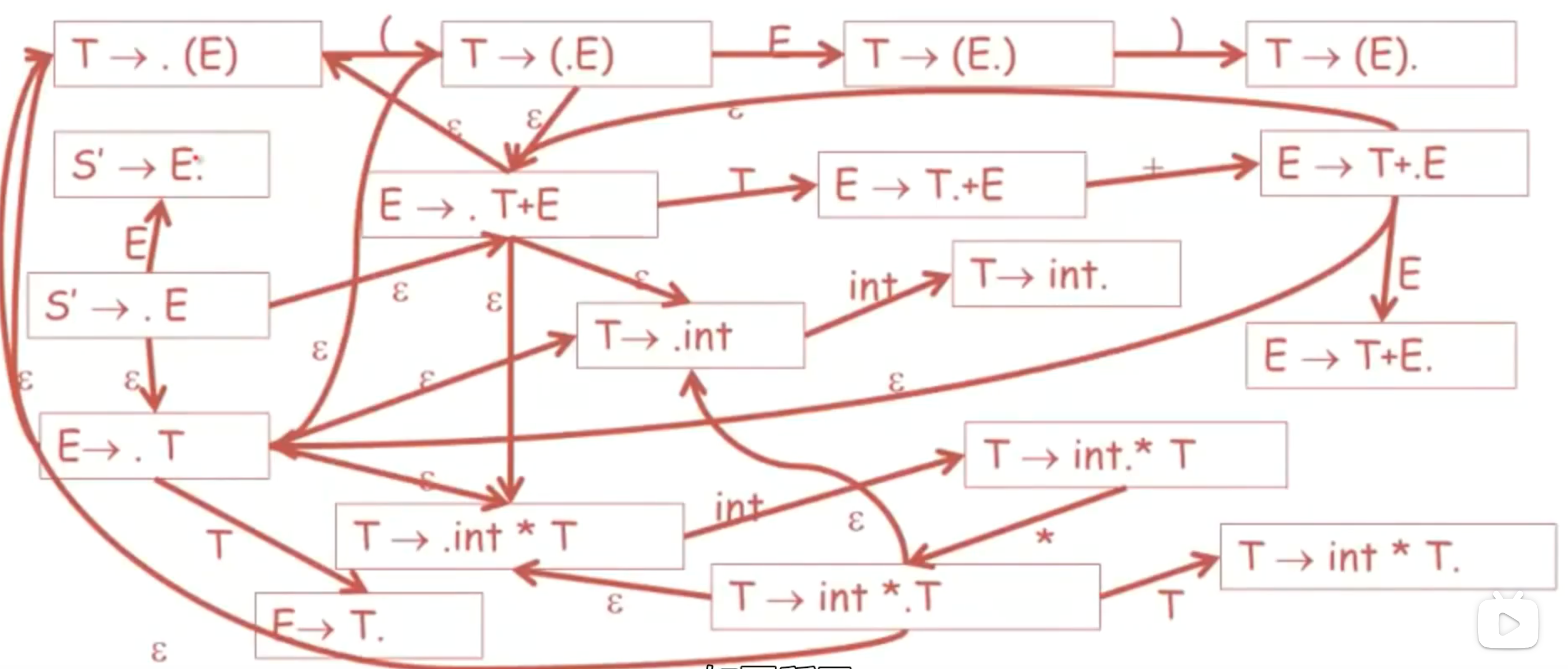他说用来识别语法可行前缀的自动机很缜密哦

$S^{'} \to . E$ 开始，我们想要的是将开始符号归约为新的开始符号。增强型。所以我们读取栈，并且希望之后在栈内看到一个E，如果没有看到。我们也希望看到某些从E推导出来的东西出现在栈内

注意我们是如何使用非确定性自动机的关键功能。我们并不知道哪一个产生式的右手边内容会出现在栈内，nfa的预测能力，接受任何可能。

valid items

使用自动机来识别可行前缀，以此引入另一个概念，valid item.有效item 使用标准的状态构造子集，构建出与非确定性自动机等同的确定性自动机

这种确定性自动机状态称为canonical collections of items or canonical collections of LR(0) items

an item is often valid for many prefixes
example:the item T→(.E) is valid for prefix ( (( ((( …

Garden of John

探索

语法分析

Abstract Syntax Trees

recursive descent parsing递归下降

RD Algorithm

define some small things used

here we go

例子

limitation of rda

the problem

Left Recursion

问题

左递归变为右递归基本形式

immediate 中间 左递归

summary

predictive parsing

使用解析表进行解析的算法

First Sets

how to construct parsing table(或者说，构建ll(1)解析表所需要的条件)

definition

algorithm sketch:

例子

Follow Sets

definition

intuition 直观方法

algorithm sketch

example

LL(1) parsing tables

目标

流程

例子

LL(1)parsing tables

bottom-up parsing

shift-reduce parsing

shift

reduce

实现

冲突

Handles

review

key question:how do we decide when to shift or reduce?

idea: want to reduce only if the result can still be reduced to the start symbol

handle的提出,what it is

informal proof 句柄只会出现在栈顶

句柄识别

news

文氏图

what does viable prefix mean?

how to compute automata that accept viable prefixes

example

the structure of the stack

example

sum

识别可行前缀 recognizing viable prefixes

算法

valid items

关系图谱

目录

反向链接

immediate 中间左递归