5-parser-cfg

编译

语法

context free grammer。该文法表达能力更强。 正则表达式也是一种文法。 四元组G={T,N,S,P} 特殊的终结符：S，开始符号。antl4 中的program; P:一条条的规则。左边替换右边。左边是单个非终结符。右边是终结符与非终结符构成的串，也可以是空串。 $A\in N--->a\in (TUN{)}^{\ast }$

E BNF extended Backus-Naur Form

+ * ? 引入这些扩展符号

• ？的表示 0或者1
• * 的表示，迭代转成递归 stats → stat stats|$ϵ$;

context-sensitive grammer(csg) 非重点

当左边不是单个非终结符时。 大B变成Z还是b取决于左边的符号

语义

上下文无关文法G定义了一个语言 L(G)

Question

语言是串的集合。 串从何来？

推导 derivation

[! info] 定义 推导即是将某个产生式的左边替换成它的右边

每一步推导需要选择替换哪个非终结符号，以及使用哪个产生式

• leftmost derivation 每一步推导都选择最左边非终结符展开
• rightmost derivation 最右推导

[! info] 定义 句型 Sentential Form 从开始符号 经过0步 或任意多步推导所得到的$\alpha$串，则称$\alpha$为文法G的一个句型。

推到头，全都是由终结符构成，最后这一步得到的字符串。

定义 句子Sentence

如果S经过0步或任意多步推导得到w串，则称w是文法G的一个句子

进行推导，凡是推导能够得出来的东西全部叫句型。最后无法再推导的叫做句子。

---

前面的铺垫

定义 文法生成的语言L(G)

文法G的语言L(G)是它能推导出的所有句子构成的集合 $L(G)=\{w|S\stackrel{\ast }{=}>w\}$

文法G的两个基本问题

Membership问题

给定字符串 x,$x\in T^{\ast }$,由终结符构成,$x\in L(G)$?,这个字符串在不在文法的语言里面。 即 检查x是否符合文法G 这是语法分析器的任务：为输入的词法单元流寻找推导、构建语法分析树、或者报错

L(G)究竟是什么？

给你一个上下文无关文法，你是否能够描述出来它所表达的语言。

这是程序设计语言设计者需要考虑的问题。

例子

S→SS S→(S) S→$ϵ$

L(G)={良匹配括号串} 看第二条，每次使用这条规则，S左右两边都加了括号。这一对括号是匹配好的。

例子

S→aSb S-<$ϵ$

L(G)={$a^n{b}^n|n\ge 0$}

反过来，

Example

字母表 $\Sigma$ = {a,b}上的所有回文串（Palindrome）构成的语言

• 写一个程序。递归的算法
• 基本的情况。不为空，展开。
• 前面产生a/b后面产生a/b。开头和结束都是a/b,看中间是否是回文串。
• 落下的情况：单个字符

{$b^n{a}^m{b}^{2n}|n\ge 0,m\ge 0$}

• 难点在于前面的b和后面的b.1个b后面两个小b
• m的个数与n没有任何关系
• a的个数与b无关，用另外一个非终结符来表示
• 右递归的方式产生任意多个小a $S\to bSbb|A$ $A\to aA|ϵ$

{$x\in {a,b}^{\ast }|x中a,b个数相同$}

$V\to aVb|bVa|ϵ$ 产生不了 aab bba.中间砍一半，左边和右边个数相同 修改： $V\to aVbV|bVaV|ϵ$ ab串可能是a开头可能是b开头，a开头后面肯定有一个小b,分成两个部分，左边右边个数相同的子串。 画一个图，最终回到x轴，a b个数相同。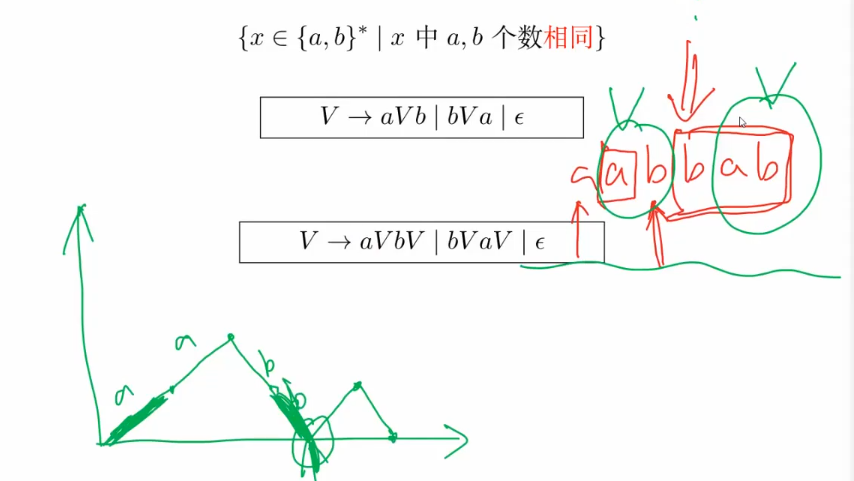

• 另一种方式， $V\to VV|aVb|bVa|ϵ$

{$x\in {a,b}^{\ast }|x中a,b个数$不同}

S\rightarrow T|U \\ T\rightarrow VaT|VaV\\ U\rightarrow VbU|VbV\\ V\rightarrow aVbV|bVaV|\epsilon \end{aligned}

• 最后一条生成相同个数的a b。
• 1 分两种情况，对称，T U，
• T 右递归 迭代，每次多出一个a。V表示相同，在字符串任意位置多插入几个a。 T表示a比较多的字符串，U表示b比较多的字符串。

---

• 中间四条。CB→BC;
• 下面四条B变小b,大C变小c
• 上面两条 每递归一次多出一个小a ,BC

---

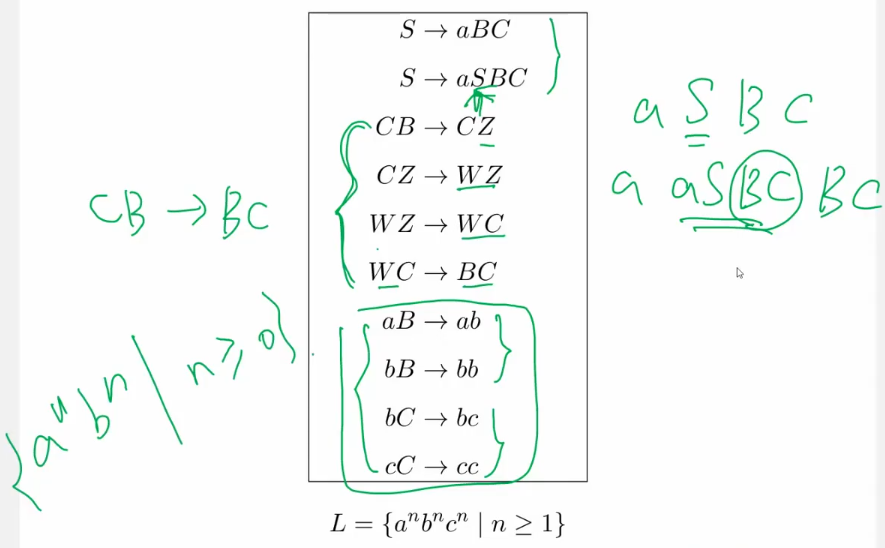
严格弱于

1. 每个正则表达式r对应的语言L(r)都可以使用上下文无关文法来描述。

非终结符 4个状态。每一个状态转移，对应一个产生式。

2. 有些语言无法使用正则表达式来描述

正规式无法描述平衡或嵌套的结构，只能表示有限的重复，一个给定结构的无线重复。

定理 Theorem

L={$a^n{b}^n|n\ge 0$} 无法使用正则表达式描述。

反证法 假设存在正则表达式 r：L(r)=L={$a^n{b}^n|n\ge 0$}. 则存在有限状态自动机D(r):L(D(r))=L设其状态数为k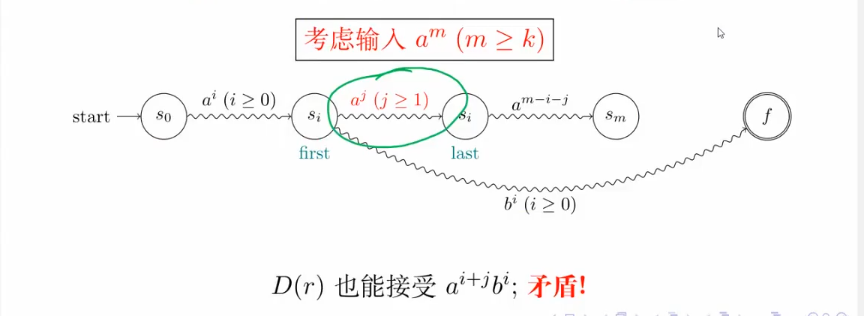$\ge 1$ 状态数目是有限的。

不停重复的一段

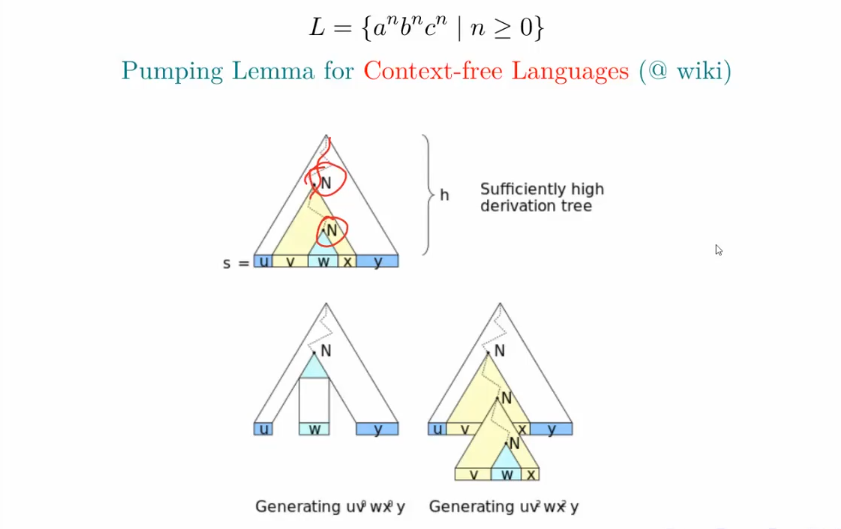
Pumping Lemma for Regular Languages

Theorem

if L is a regular language,then there exists a number p $\ge$ 1(pumping length) such that any string s in L of length $\ge$ p can be divided into three pieces**,s=xyz**,satisfying the following conditions: (i) |y| $\ge$ 1 (ii) |xy| $\le$p (iii) $\forall i\ge 0:x{y}^{i}z\in L$

p :dfa的状态个数，只是存在，只有它足够长

• 第一条性质：重复状态的长度大于等于1的

Example

D={$1^{n^2}|n\ge 0$} is not regular.

不可能满足三个条件。

---

两个相同的树 两个相同的状态