今日主题：LR语法分析器
- ll1：自顶向下，递归下降，预测分析
- 弱点：在仅看到右部的前k个词法单元时就必须预测要使用哪条产生式.没有看到完整部分。
- lr(k)的优点：看到某个产生式的整个右部对应的词法单元之后再决定。要不要做后续动作。归约。
概括：自底向上的，不断归约的，基于句柄（找完整的右部）识别自动机的，
1.框架
自底向上构建语法分析树
根节点是文法的起始符号S
每个中间非终结符节点表示使用它的某条产生式进行归约
叶节点是词法单元流w$
仅包含终结符号与特殊的文件结束符
最右推导的逆过程 归约，
L：从左向右 left-to-right扫描输入 R：构建反向(reverse) 最右 (right) 推导；
一个好的语法分析算法 线性 当读完输入后整个语法分析树就构建起来了。而不是读完之后才开始建立。所以不能最左推导反过来。
LR语法分析器的状态
分为两个部分，未读取和已构建好的语法分析树的上边缘。 在任意时刻，语法分析器的上边缘与剩余的输入构成当前句型。 使用栈结构保存上边缘。
栈上的操作
两大操作：移入输入符号；按产生式归约 直到栈中仅剩开始符号E，且输入已结束，则成功停止
两个问题
1. 何时归约？（何时移入）
取决于栈的状态。用一张表来指导。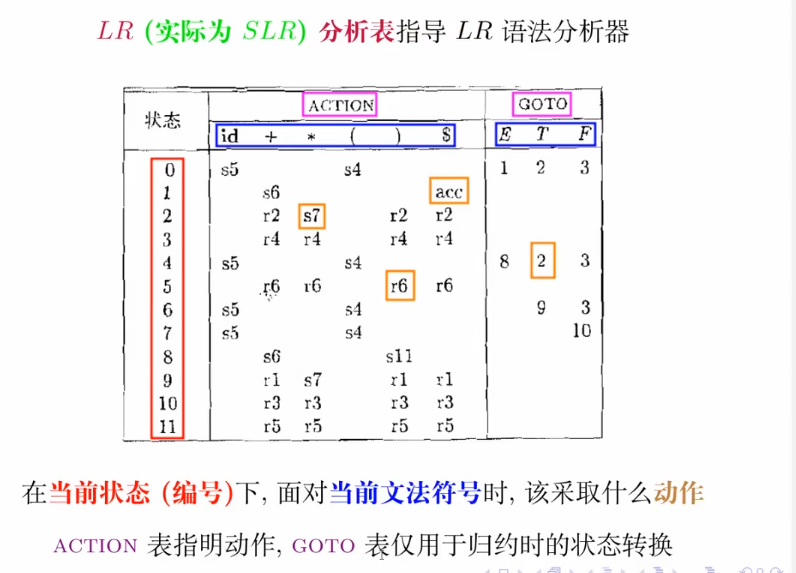
| 符号 | 语义 |
|---|---|
| sn | 移入输入符号，并进入状态n |
| rk | 使用k号产生式进行归约 |
| gn | 转换到状态n |
| acc | 成功接受，结束 |
| 空白 | 错误 |
| 数字表示 状态x，产生式x | |
| w=id*id$ |
2. 按哪条产生式进行归约？
- 必要条件：当前状态中，已观察到某个产生式的完整右部
如何构造LR分析表
在当前状态（编号）下，面对当前文法符号时，该采取什么动作？
状态是什么？如何跟踪状态？
状态是语法分析树的上边缘，存储在栈中，每加一个或者每弹出一个符号，状态变化。
句柄
Definition
在输入串的（唯一）反向最右推倒中，如果下一步是逆用产生式 将归约为A，则称是当前句型的句柄。
LR语法分析器的关键就是高效寻找每个归约步骤所使用的句柄。
句柄可能在哪里？
设计一种满足“句柄总是出现在栈顶”性质的LR语法分析器
handle-finding automaton 自动机两个要素：自动机的状态是什么？自动机之间的状态是如何跳转的？
项 项集 项集族
状态刻画了当前观察到的针对所有产生式的右部的前缀
为了表示产生式的右部的前缀，引入了项的概念，
Item
文法G的一个LR(0)项是G的某个产生式加上一个位于体部的点
项 指明了语法分析器已经观察到了某个产生式的某个前缀
Example
A→.XYZ 刚开始决定跟踪，看到了0个前缀 A→X.YZ 观察到了大X A→XY.Z A→XYZ. 观察到了完整的右部 特殊情况：A→只有一个项[A→.]
项集
项集就是若干项构成的集合
因此，句柄识别自动机的一个状态可以表示为一个项集
项集族：若干项集的集合。
因此，句柄识别自动机的状态集可以标识为一个项集族
增加文法
[! tip] 增广文法(Augmented Grammar) 文法G的增广文法G’是在G中加入产生式S’→S得到的文法。
- 目的：告诉语法分析器何时停止分析并接受输入符号串；表示算法结束。
- 语法分析器当前栈中仅有S且面对$,要使用S’→S进行归约时，输入符号串被接受
开始状态
E’→.E
期望看到大E，然后结束。
点指示了栈顶，左边（与路径）是栈中内容，右边是期望看到的文法符号串。
期望观察到大E，也是在期望观察到E+T，也是在期望观察到T，因为大E是这两种可能性，同时追踪他们。
同时跟踪所有的这些产生式的右部
closure({[E’→.E]})
状态的转移
注意的点：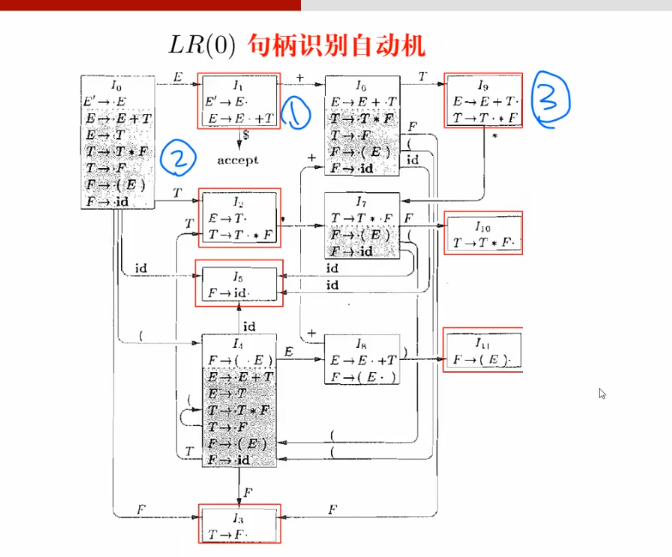
- 接受状态，E+$ acc
- 可以接受非终结符 T
- 红框：存在一个产生式已经跟踪完了，说明看到了一个句柄。接受状态。
LR(0)分析表构造规则总结
- 终结符 shift;非终结符 goto
- [k:A\rightarrow\alpha .]\in I_i \wedge A\neq S' \Rightarrow\forall t \in T\cup\{\}.ACTION[i,t]=rk$
- [S'\rightarrow S.]\in I_i\Rightarrow ACTION[i,\]\leftarrow acc$ 归约，第四个特殊的归约，增广产生式。
LR(0)文法
每个表只填一个动作，如果文法G的LR(0)分析表是无冲突的，则G是LR(0)文法。
- 0的含义：归约的时候不需要向前看。
LR(0)自动机与栈之间的互动关系
向前走 移入
回溯归约
自动机才是本质，找到句柄，栈是实现方式。（用栈来记住来时的路，以便回溯）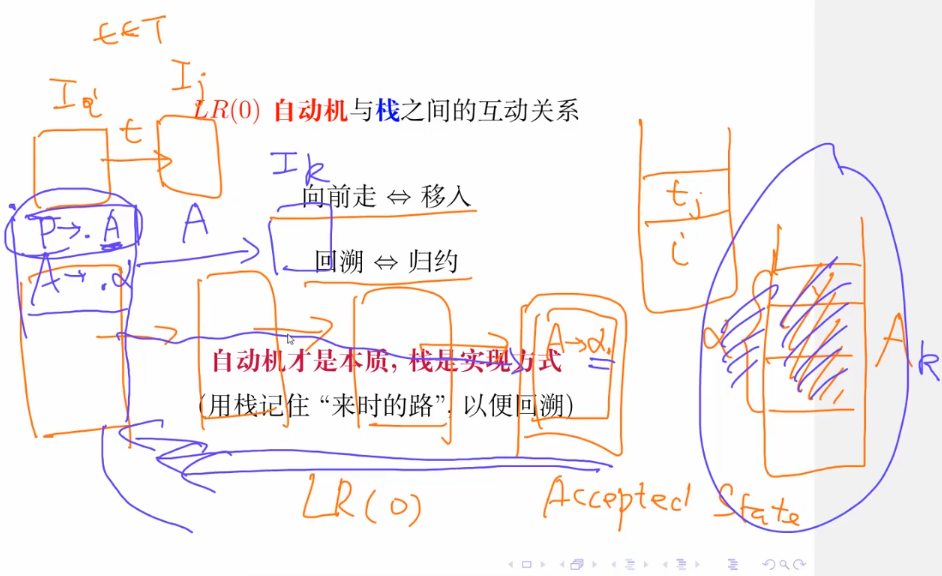
栈上看到了alpha,右端弹出去，push A,对应自动机 ，回溯。回到状态。P→.A非终结符展开变成A→..通过大A 转移到某个状态k.现在的栈对应的状态为k.