Skip to content

绪论

计算

  • 研究对象：规律、技巧，过程规律方法
  • 研究目标：高效计算、低耗

cs (手段)should be called computing science,for the same reason why surgery is not called knife science. -dijkstra

  • 绳索计算机及其算法 12 垂直 3点的环
  • 尺规计算机及其算法 机械地执行……
  • 算法 *计算=信息处理
  • 借助某种工具，遵照一定规则，以明确而机械的形式进行
  • 计算模型=计算机=信息处理工具
  • 算法，及特定计算模型下，旨在解决特定问题地指令序列
    • 输入：问题；输出：答案；
    • 正确性；确定性；可行性（大象冰箱）：每一基本操作都可实现，且在常数时间内完成
    • 有穷性：hailstone 27 程序未必是算法
  • 好算法 正确 健壮（不合法做处理）可读（结构化 准确命名 注释）效率： 既要马儿快快跑，又要马儿吃得少 算法+数据结构=程序 N.wirth,1976 狗尾续貂……（算法+数据结构）*效率（非简单堆砌）=computation

计算模型

度量 一把尺子标有刻度> to measure is to know.if you cannot measure it,you cannot improve it. -lord kelvin

  • 算法分析
  • 正确性；成本（性能）如何度量如何比较 如何归纳概括 分类 问题实例的规模往往是决定计算成本地主要因素最坏情况 成本最高 算法 输入（规模类型）程序员语言编译器 硬件：体系结构 软件：操作系统 引出理想平台或模型
  • turing machine
  • tape
  • alphabet
  • head 功能 读写
  • state 经过一个节拍 转向另一个状态
  • transition funtion 状态h停机
  • ram *寄存器顺序编号 加减，赋值 二者是一班计算工具的简化和抽象，使我们独立于具体的平台 在这些模型中 运行时间转换 基本操作次数

大o记号 直尺的刻度

mathematics is more in need of good notations than of new theorems. 好读书不求甚解。 看重长远，更大规模，主流。 长远:n足够大 主流：非主流常系数低次项可忽略 上界悲观估计 Ω 下界 T(n)>cf(n) θ 确界

  • 刻度1 常数o(1)
  • 刻度2 对数o 常底数无所谓 loga n=loga b*logb n
  • 刻度3 多项式n的 c次方
  • 刻度4 线性 O(n)
  • 刻度5 指数 2的n次方 2 subset NP-complete

算法分析

通过挖掘不变性和单调性来证明正确性

  • 迭代：级数求和
  • 递归：递归跟踪+递推方程
  • 猜测+验证

级数

  • 算术级数：与末项平方同阶
  • 幂方级数:比幂次方高1
  • 几何级数：与末项同阶,a>1 (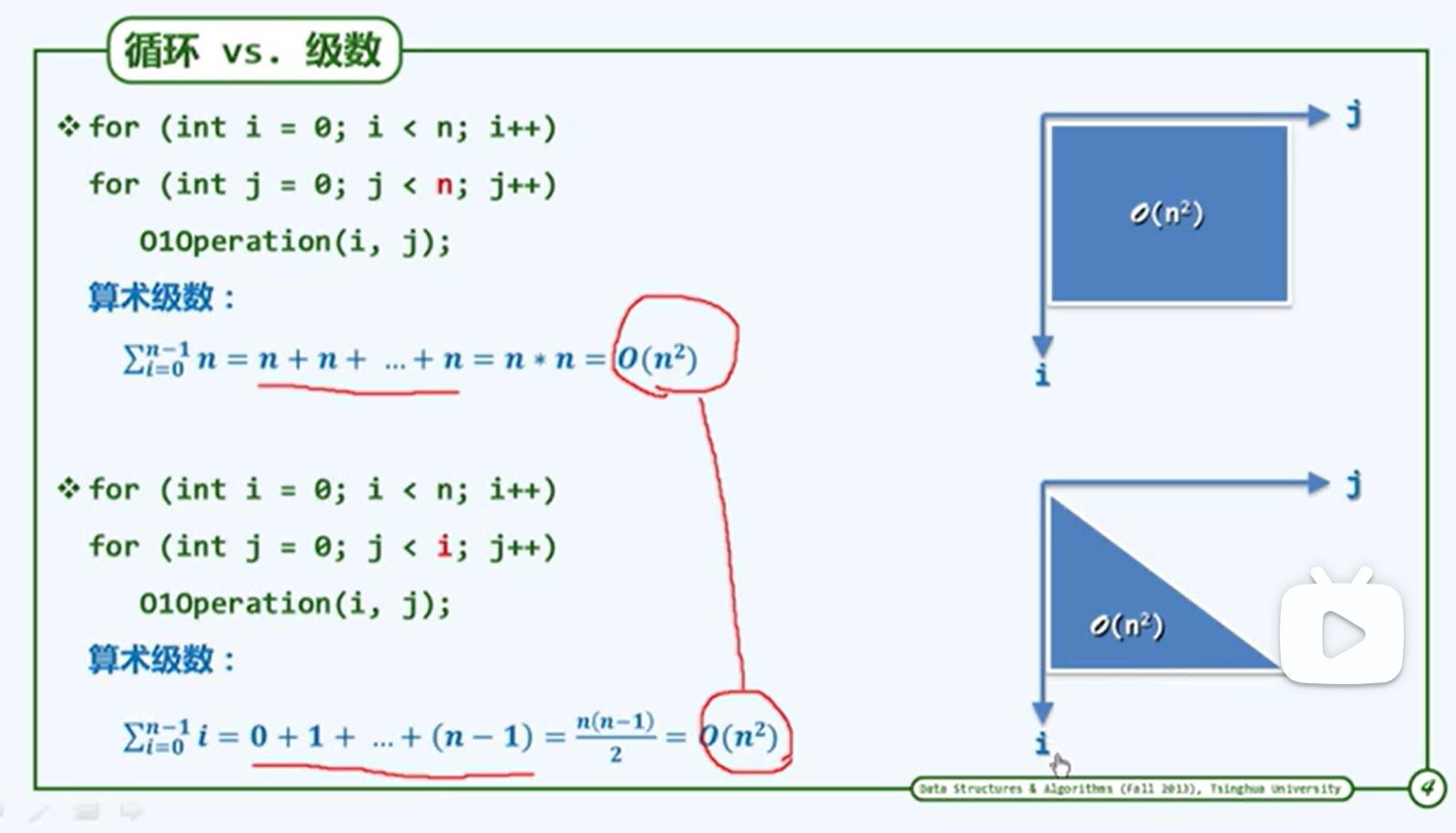alt text) 与上图做对比 alt text
i<<=1 //左移一位 二进制

冒泡排序

  • 不变性：k轮扫描交换后，最大的k个元素必然就位
  • 单调性：k轮扫描交换后，问题规模缩减至n-k
  • 正确性： 之多经过n趟扫描

封底估算back-of-the-envelope calculation

费米 纸 原子弹爆炸当量 古希腊 地球直径 对时间 1day=24hr*60min*60sec=10^5 sec 1life=1century=100yr*365=310^4day=3*10^9sec 三生三世=300yr=10^10 三生三世中的一天=一天的一秒 宇宙大爆炸至今=10^21 考察对全国人口普查数据的排序 alt text 算法改进的威力

迭代和递归

to iterate is human,to recurse,divine ?

  • 减而治之 规模缩小+平凡问题 递归基 *数组倒置

```c++ void reverse(int* A,int lo,int hi); if (lo)//low high 之间有足够多的元素,问题规模奇偶性不变，每次减2，需要两个递归基

  • 分而治之

``` 数组求和:二分递归 

sum(int A[],int lo,int hi){

  //区间范围【L,h】
  if (lo==hi)return A[LO];
  int mi=(lo+hi)>>1;//chuyi2
  return sum(A,lo,mi)+sum(A,mi+1,hi);//入口形式为sum(A,0,n-1)








}

算法所需时间 几何级数 * Max2:迭代一 从数组区间A[lo,hi]中找到最大两个整数A[]和A[] 循环扫描，三重，扫描前后 x1得到 o(2n-3) M:二

```c++
void(int A[],int lo,int hi,int &x1,int &x2){
  if(A[x1=lo]<A[x2=lo+1])swap(x1.x2);//initial
  for(int i=lo+2;i<hi;i++>)
    if(A[x2]<A[i])
      if(A[x1]<A[x2=i])
        swap(x1,x2);


}


```

alt text

Max2:递归+分治